*Expand the Hamiltonian to Quadratic Order.
*Fourier transform the Hamiltonian into momentum space.
*Identify the Brillouin zone (range of distinct ks).
*Rewrite the Hamiltonian in terms of creation and annihilation operators.
*Obtain the Spectrum.
*Compute the Density of States.
*Use the Planck distribution to obtain the thermodynamics of the vibrationalmodes of the crystal.
Discrete Translational Invariance:
The Reciprocal Lattice, Brillouin Zones, CrystalMomentum.
Note that, in the above, momenta were only de ned up to (2.pi.n)/a . The momenta (2.pi.n)/a form a lattice in k-space, called the reciprocal lattice. This is true of any function which, like the ionic discplacements, is a function de ned at the lattice sites. Forsuch a function, f(R), de ned on an arbitrary lattice, the Fourier transform
satisfiesif G is in the set of reciprocal lattice vectors, de ned by:

The reciprocal lattice vectors also form a lattice since the sum of two reciprocal lattice vectors is also a reciprocal lattice vector. This lattice is called the reciprocal lattice or dual lattice. In the analysis of the linear chain, we restricted momenta to k< (pi/a) to avoiddouble-counting of degrees of freedom. This restricted region in k-space is an example of a Brillouin zone (or a rst Brillouin zone). All of k-space can be obtained bytranslating the Brillouin zone through all possible reciprocal lattice vectors. We could have chosen our Brillouin zone di erently by taking 0 < k < (2pi/a). Physically,there is no diference; the choice is a matter of convenience. What we need is a set of points in k space such that no two of these points are connected by a reciprocal latticevector and such that all of k space can be obatained by translating the Brillouin zonethrough all possible reciprocal lattice vectors. We could even choose a Brillouin zonewhich is not connected, e.g. 0 < k < (pi/a). or (3pi/a) < k < (4pi/a).
Later, we will consider solids with a more complicated lattice structure than ourlinear chain. Once again, phonon spectra will be de ned in the Brillouin zone. Since f(k)= f(k + G), the phonon modes outside of the Brillouin zone are not physically distinct from those inside. One way of de ning the Brillouin zone for an arbitrary lattice is to take all points in k space which are closer to the origin than to anyother point of the reciprocal lattice. Such a choice of Brillouin zone is also called theWigner-Seitz cell of the reciprocal lattice. We will discuss this in some detail laterbut, for now, let us consider the case of a cubic lattice. The lattice vectors of a cubiclattice of side a are:
The reciprocal lattice vectors are:The reciprocal lattice vectors also form a cubic lattice. The rst Brillouin zone(Wigner-Seitz cell of the reciprocal lattice) is given by the cube of side (2pi/a) centeredat the origin. The volume of this cube is related to the density according to:
As we have noted before, the ground state (and the Hamiltonian) of a crystal is invariant under the discrete group of translations through all lattice vectors. Whereas full translational invariance leads to momentum conservation, lattice translationalsymmetry leads to the conservation of crystal momentum { momentum up to a reciprocal lattice vector. (See Ashcroft and Mermin, appendix M.) For instance, in a collision between phonons, the di erence between the incoming and outgoing phonon momenta can be any reciprocal lattice vector, G. Physically, one may think of the missing momentum as being taken by the lattice as a whole. This concept will alsobe important when we condsider the problem of electrons moving in the backgroundof a lattice of ions.
Lattice Structures
Thus far, we have focussed on general properties of the vibrational physics of crystalline solids. Real crystals come in a variety of di erent lattice structures, to whichwe now turn our attention.




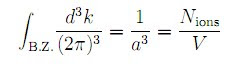
No hay comentarios:
Publicar un comentario